機械学習/naive Bayes model - 鯨飲馬食 @ wiki

メニュー

更新履歴

取得中です。

この項の問題点
概要
EMアルゴリズムによるパラメータ推定

この項の問題点

この項は未完成であり重大な間違いを含んでいる可能性があります。（2009-08-09）

概要

naive Bayes modelはクラスが与えられた時、各attributeが条件付独立となるモデルです。（naiveがかかるのはmodelであってBayesではありません。念のため。）
$c$ と $attr$ の同時確率は以下の式で表されます。

$\begin{eqnarray} p(C=c,Attr=attr) &=& p(C=c, Attr_1=attr_1 , \ldots , Attr_J=attr_J) \\ &=& p(C=c) \prod^{J}_{j=1} p(Attr_j=attr_j \mid C=c) \\ \end{eqnarray}$

以下はBayesian networkでの表現です。

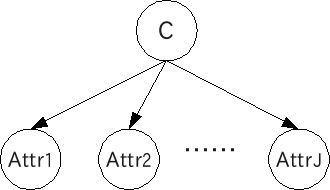
EMアルゴリズムによるパラメータ推定

$\begin{eqnarray} p(X=k , {\bf Y}={\bf y} \mid \theta) &=& p(X=k \mid \theta) p({\bf Y}={\bf y} \mid X=k , \theta) \\ &=& p(X=k \mid \theta) \prod_{j=1}^{J} p(Y_j=y_j \mid X=k , \theta) \end{eqnarray}$

EMアルゴリズムの $Q(\theta' \mid \theta)$ は以下の形。

$\begin{eqnarray} Q(\theta' \mid \theta) &=& \sum_{t=1}^{T} \sum_{k=1}^{K} p(k \mid {\bf y}_t , \theta) \log p(k, {\bf y}_t \mid \theta') \\ &=& \sum_{t=1}^{T} \sum_{k=1}^{K} p(k \mid {\bf y}_t , \theta) \left( \log p(k | \theta') + \sum_{j=1}^{J} \log p(y_{t,j} \mid k , \theta') \right) \\ &=& \sum_{t=1}^{T} \sum_{k=1}^{K} p(k \mid {\bf y}_t , \theta) \log p(k \mid \theta') + \sum_{j=1}^{J} \sum_{t=1}^{T} \sum_{k=1}^{K} p(k \mid {\bf y}_t , \theta) \log p(y_{t,j} \mid k , \theta') \end{eqnarray}$

$p(k \mid \theta)$ はcategorical distributionにしたがうとします。
つまり $p(k \mid \theta) = \pi_k$ と表し、 $\sum_{k=1}^{K}\pi_k = \sum_{k=1}^{K}p(k \mid \theta) = 1$ を満たします。
mixture modelの時と同様に更新式は以下の形になります。

$\begin{eqnarray} && {\pi'}_k \propto \sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta) \end{eqnarray}$

ある $j$ において $p(y_j \mid k , \theta)$ がcategorical distributionにしたがう場合を考えます。
$p(y_j = m \mid k , \theta) = \phi_{k,m}$ と表し、 $\sum_{m=1}^{M}\phi_{k,m} = \sum_{m=1}^{M}p(y_j = m \mid k , \theta) = 1$ を満たします。
$p(k \mid \theta)$ と同様に更新式は以下の形になります。
ただし $\delta(y_{t,j} = m)$ は $y_{t,j} = m$ を満たす時1を、それ以外は0をとるとします。

$\begin{eqnarray} && {\phi'}_{k,m} \propto \sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta) \delta(y_{t,j} = m) \end{eqnarray}$

ある $j$ において $p(y_j \mid k , \theta)$ が多次元正規分布(multivariate normal distribution)にしたがう場合を考えます。

$\begin{eqnarray} && p(y_j \mid k , \theta) = {\cal N}(y_j \mid \mu_{j,k} , \Sigma_{j,k}) = \frac{1}{(2\pi)^{D/2} \mid \Sigma_{j,k} \mid ^{1/2}} \exp \left(- \frac{1}{2} (y_j-\mu_{j,k})^{\rm T} \Sigma_{j,k}^{-1} (y_j-\mu_{j,k}) \right) \end{eqnarray}$

これもmixture modelの時と同様です。

$\begin{eqnarray} {\mu'}_{j,k} = \frac{\sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta) y_{t,j}}{\sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta)} \end{eqnarray}$

$\begin{eqnarray} {\Sigma'}_{j,k} = \frac{\sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta)(y_t-{\mu'}_{j,k}) (y_{t,j}-{\mu'}_{j,k})^{\rm T}}{\sum_{t=1}^{T} p(k \mid {\bf y}_t , \theta)} \end{eqnarray}$

タグ：

+ タグ編集

「naive Bayes model」をウィキ内検索

最終更新：2010年01月21日 08:02

添付ファイル

NB_BN.png